Measuring Distances – the “Distance Ladder”
A question we are often asked when we display the wonderful images taken by our members is ‘how far is away is that galaxy”. The answer is invariably a huge number in the order of hundreds of millions of light years away. Have you ever wondered how astronomers determine these distances?
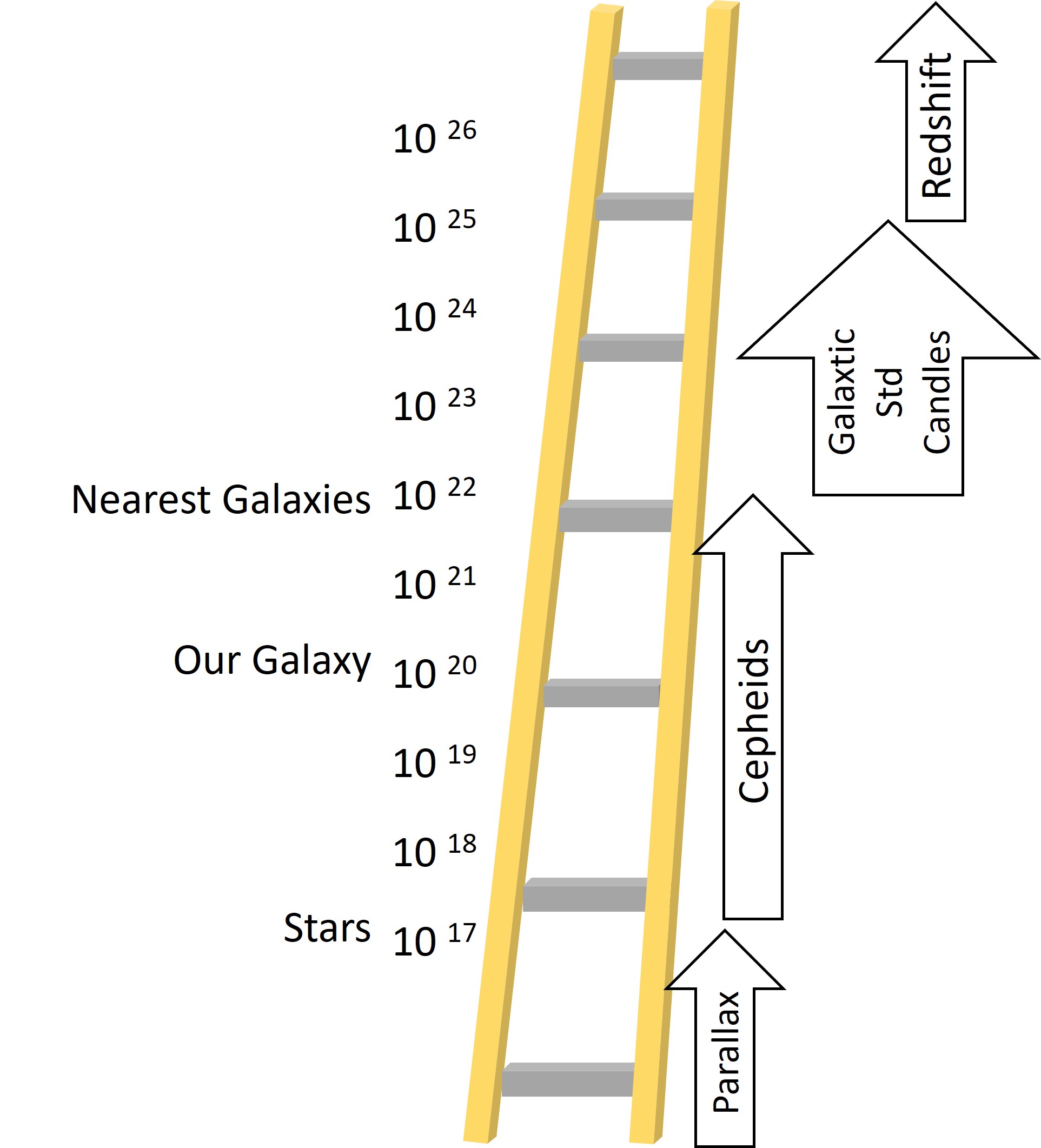
In fact, astronomers will use different methods to estimate distances depending on how distant the object is. Some methods of estimating distances work only on objects that are relatively close to us, others are suitable only for huge intergalactic distances. When we refer to the “Distance Ladder” we are referring to a succession of techniques, by which distances are established first to stars in the solar neighbourhood, then to more distant stars in our galaxy, and then to other nearby galaxies.
Some of these techniques are described below.
Trigonometric Parallax
This is the first rung on the distance ladder and uses the apparent displacement of positions of nearby stars as the earth orbits. You can see the effect of parallax if you hold up a at arms length in front of you. Now alternately close each eye. Your finger will “move” when compared to a more distant object (see figure below).
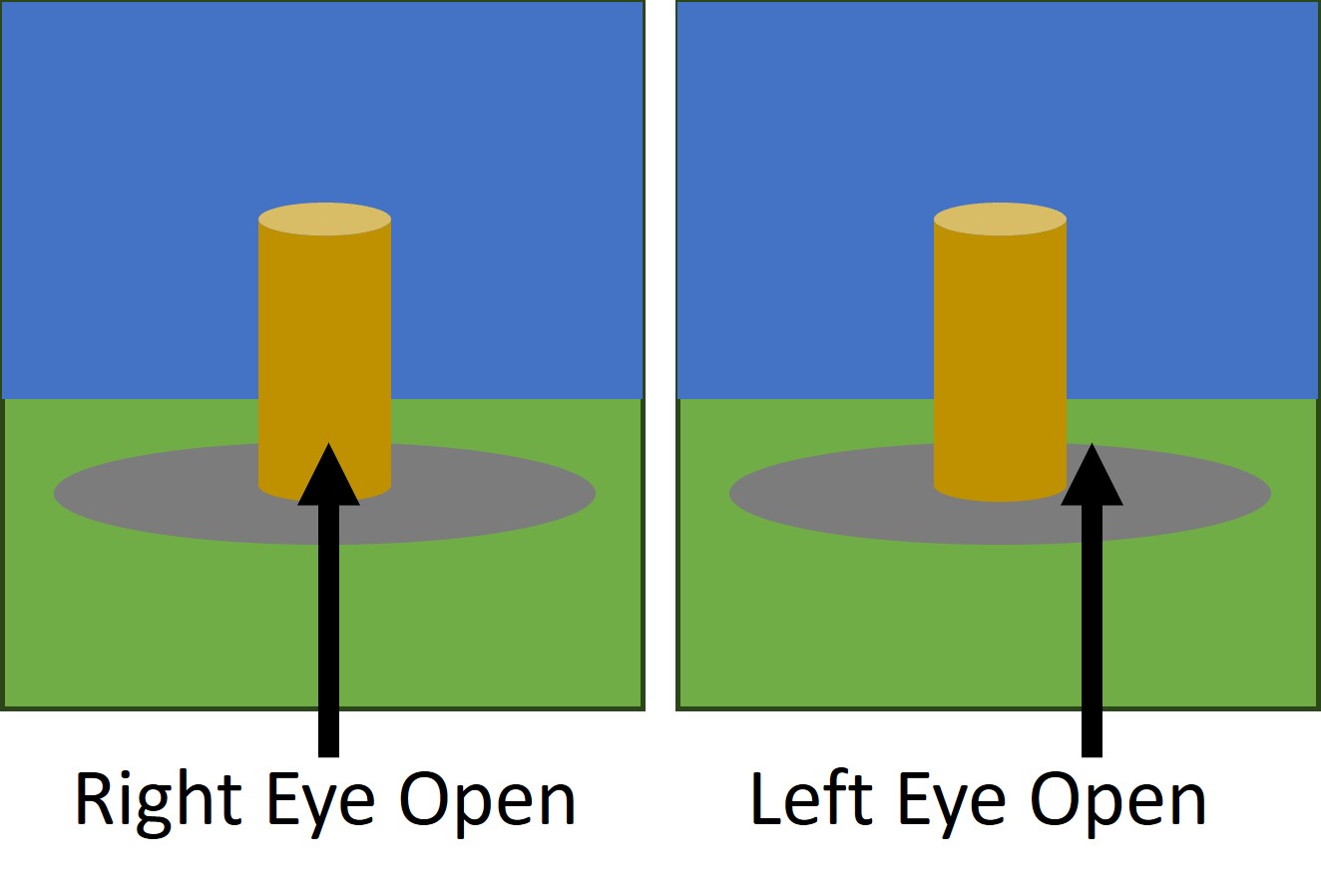
The motion of the Earth around the Sun causes an apparent motion or parallax of nearby stars against the background of more distant objects if we observe the object at opposite sides of the sun. The amount of apparent motion, expressed as the change in angular position on the sky, depends on the distance to the observed object and the length of the observation baseline (the distance between the two points where you measure the angles).
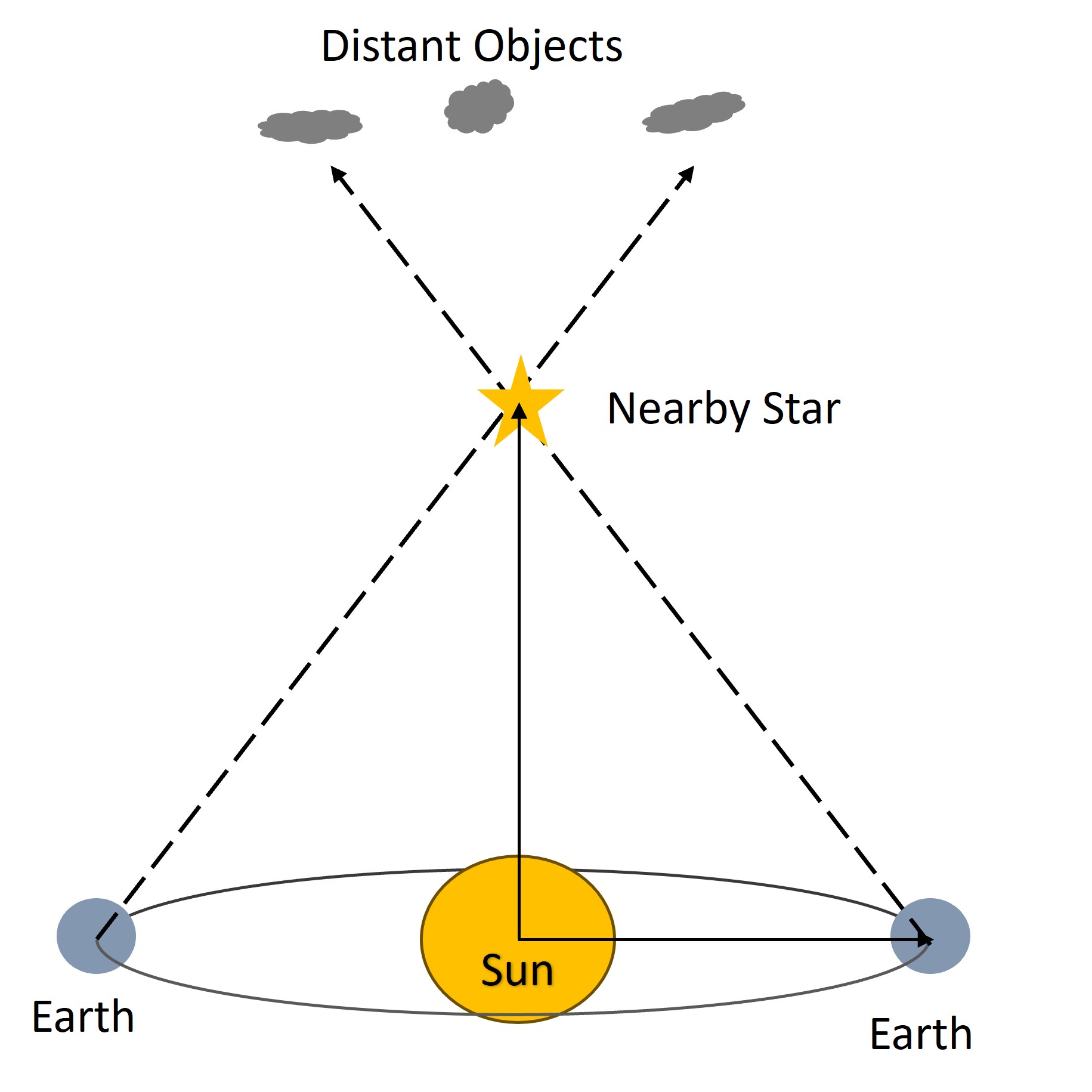
This is shown in the diagram above, but the angles are exaggerated hugely (because I don’t have a screen that is tens of light years in length). For a very small angle ‘a’ then a = r / d. The distance r is 1 Astrometrical Unit (1AU) – about 150 million kilometres. We define a parsec as the distance to than an object would appear to move by 1 arcsecond (1/3600 of a degree) against distant galaxies when the Earth moves 1AU (or to put it another way, the parsec is the distance at which 1 AU subtends 1 arcsecond. So an object located at 1 parsec would, by definition, have a parallax of 1 arcsecond).
The parsec is a very convenient unit of measure because woring in these units:
distance (in parsecs) = 1 / parallax angle (in arcseconds)
One parsec is equal to 3.26 light years or, if you like big numbers, about 31 trillion kilometers. (According to wikipedia the first documented use of the term parsec was in 1913 and is attributed to Herbert Hall Turner, a British astronomer and seismologist.)
The problem with this method is that the angles are vey small indeed and difficult to measure making it suitable for objects that are relatively close to us. The Hipparcos satellite measured distances of 2.5 million stars to a distance of 150pc and the brightest stars to distances of 1,000pc. Even at 1,000pc (1kpc) we are still well within our own Milky Way galaxy (diameter approximately 30kpc)
Standard Candles
A standard candle is an astronomical object, perhaps a star or galaxy, for which one of its intrinsic properties is already known (e.g. its absolute luminosity or actual size). For example, if the actual size of an object is known (it rarely is) then using the observation of its apparent size in the sky and simple trigonometry will allow us to calculate its distance. Similarly, if we have an object of known brightness then it’s distance can be calculated by comparing the known luminosity to its observed brightness (using the inverse square law). Examples of standard candles commonly user by astronomers include Cepheid variables, RR Lyrae stars and supernovae.
Cepheid variables are an extremely important as standard candles because they are relatively numerous, bright and distinctive. The average luminosity of a Cepheid during its cycle correlates extremely well with the period of the oscillation. Our understanding of the cepheid period-luminosity relation is based on what we can measure accurately. The precision of distance measurements based on the period-luminosity relation depends primarily on the precision with which the distance of some Cepheids is known. The latest data uses trigonometric parallaxes determined by the Hipparcos satellite. So we can see that how the second rung of our distance ladder follows the first.
There are fundamental two problems with using the luminosity of an object as a standard candle. The first is the assumption that we know the actual luminosity of the object, and the second is applying an appropriate correction for the absorption of light by intervening dust which will cause the light to diminish more quickly than the inverse square law. For cepheids in particular, there is also some debate about how the metallicity of a cepheid (the proportion of its matter the made up of elements with an atomic number greater than Helium) affects the period-luminosity relation.
Main Sequence Fitting
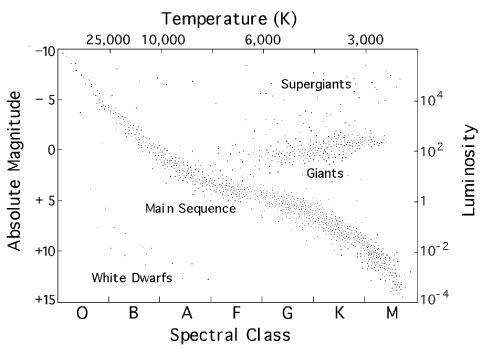
When the absolute magnitude for a group of stars is plotted against their spectral classification (a Hertzsprung-Russell diagram) very clear patterns are found that relate to the mass, age and composition of the star. When stars are burning hydrogen they lie along a curve in the diagram called the Main Sequence. We can determine a star’s position on the main sequence from its star spectrum and thereby estimate the star’s absolute magnitude.
Galactic Standard Candles
As stated above, the observation of Cepheid variables in nearby galaxies allows the calculation of their distance. However, we can resolve individual stars only in our own and nearby galaxies. To measure the distance to galaxies at greater distances we either need much brighter standard candles or techniques that do not need us to observe individual stars. The candidates for brighter standard ‘galaxtic’ candles are:
- Type Ia supernovae
- Galaxies
One model for the formation of this category of supernova is a close binary star system where the larger of the two stars is the first to evolve off the main sequence and eventually becomes a white dwarf star. Eventually the secondary star also evolves off the main sequence to form a red giant. Matter from the giant is accreted by the white dwarf, causing the white dwarf to increase in mass until it reaches its Chandrasekhar limit of 1.4 M solar masses. The white dwarf then becomes unstable and explodes. As all type Ia supernovae are caused by the explosion of stars of the same mass (1.4 solar masses), they should all have the same luminosity.
Of course, with greater distances there is more uncertainty about the degree of extinction of light by dust – and there are other potential models for the causes of Type 1a supernovae.
Redshift
On scales well beyond our nearby galaxies astronomers use cosmological redshift to calculate distances. While observing the redshifts of a large number of galaxies with distances determined using the above techniques Edwin Hubble discovered that the further the galaxy from our own, the greater its redshift. The Hubble Constant quantifies the current rate of expansion of the universe and gives us a linear relationship between recessional velocity and distance..
Hubble made this discovery when he combined own measurements of galaxy distances based on the period-luminosity relationship for Cepheids with existingmeasurements of the redshifts associated with the galaxies. The key point here being that Cepheids provided the empirical step up the ladder to a technique for measuring even larger distances.
Redshift (and hence recessional velocity) can be measured accurately using spectroscopic techniques but the distances calculated on the basis of recessional velocity are sensitive to certain ‘uncertainties’. Firstly, there are three types of redshift:
- Doppler redshift caused by a body’s relative motion away from us
- Cosmological redshift caused by the expansion of the universe
- Gravitational redshift caused by gravitational fields
Again, systemic errors can creep in. The recessional velocity estimated using redshift is an apparent velocity and will include an element of some or all of these. Secondly, there is still some small uncertainty in the value of the Hubble Constant (but WMAP has brought the error bounds down to about 2%).
Summary
Parallax is the only direct means of measuring distance and is independent of the properties or intrinsic brightness of the object measured. Methods described above based on the absolute magnitudes of standard candles, are ‘secondary’ because they rely on distances established by the primary parallax technique. For example the Cepheid period-luminosity relationship is calculated using data from primary techniques and is then applied to stars in nearby galaxies. In this way the Distance Ladder is constructed. The Distance Ladder bases the measurement of successively greater distances on estimates made at smaller scales.
by Peter Campbell-Burns
Jul 2010
