Another look at the Twins Paradox
The Twins Paradox – aargh, the Twins Paradox! The familiar version of this is based on a thought experiment where one twin shoots off on a journey through space at close to the speed of light and travels for some years. When he or she returns, they find that their twin, who remained on Earth, has aged considerably but they have not. The returning twin is much younger than the one who stayed behind. This is enough of a paradox for me – but Andrew Collins in his excellent talk on an introduction to Relativity – explained how it is even more paradoxical than that.
Before we can get into the Twins Paradox, we need to understand some of the ideas underpinning the theory of relativity. The key is that the speed of light is constant and not dependent on the motion of the light source. This is a very inconvenient fact if you like everything to be neat, tidy and easy to understand as in Newton’s world of motion. It has though been put to numerous experimental tests and it is a fact which has to be faced. Grrr!
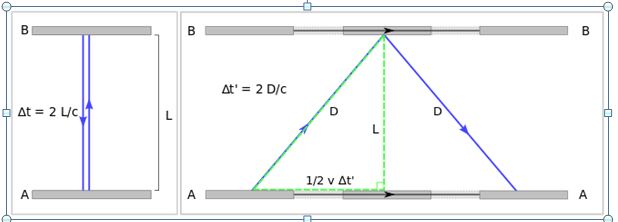
Time dilation
One consequence of the speed of light being constant is time dilation. A thought experiment is again used to explain this.
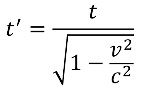
Imagine you are in a container and there is a pulse of light starting at A being directed to a mirror at B, reflecting back to A. The time for the round trip is given by a re-arrangement of the formula speed = distance/ time, familiar from so many school lessons. Now imagine your container is moving at a constant speed v from left to right. You are unaware of this motion as you are “stationary” within it but, to an observer outside, the event looks very different. (It is very significant that you and your container are moving at a constant speed. More on this later!). The observer sees the pulse of light travelling diagonally up to the mirror and diagonally back down again. It travels a longer distance … but the observed speed of the light is the same!! The only way this can come about is for the observed time for the “A-B-A” journey to be longer. This is what is referred to as time dilation ; much more time has passed for the observer than for you. Applying Pythagoras Theorem, also familiar from school lessons, with some re-arrangement leads to this formula for the extent of time dilation.
The faster the container is travelling, the larger v, the closer the v2/c2 term approaches to 1 and the smaller the denominator, making t’ greater and greater.
Thought experiments are all well and good but they need to be backed up by experimental results. There have been many experiments which show time dilation to be a reality. These include flying atomic clocks round the world and comparing their displayed time on return with one which never left the ground. The results agree closely with the predictions of Special Relativity. Another example was muon lifetime. Andrew in his talk illustrated this point by reference to muon life-time in a particle accelerator – they can do far more laps than expected given their very short life-time. Their “internal clock” is ticking fast; we observed a time dilated effect so that short life-time is extended, giving them time to do many laps.
The Twins Paradox
Now for the twins! Let’s call them Jack and Jill, just to avoid awkward uses of personal pronouns. Jack is staying on Earth and Jill is going on a long journey through space and returning. Let’s say that she travels to a place 6 light years away at such a speed that it takes her 8 years. She will have aged 16 years by the time she returns. But that 16 years to Jack, observing it, will be much greater due to time dilation by a factor of over 2 using the values I have chosen. He will have aged 36 years! He will now be older than his twin.
This idea of a returning twin being younger than a stay-at-home twin is common across the internet and was, I confess, the extent of my awareness of the twins paradox. Not so! It is even more paradoxical than that, as Andrew enlightened me in his talk. Well, perhaps “enlightened” is putting is a bit strongly ; though that is a reflection on me, rather than Andrew!
To understand the full paradox, you need to think of the journey from JILL’S point of view. She is stationary relative to her spaceship (the spaceship is flying at a constant speed ) and it is JACK who is moving quickly away from her and then returning. So it can be argued that JACK only ages by 16 years while JILL ages by 36 years. In other words, the returning twin is either younger than or older than the other twin depending on the frame of reference you take; even in the often surreal world of relativity, this cannot possibly be correct.
Much googling of explanations has revealed several possibilities and – surprisingly – quite a few refutations of the whole basis of relativity. The explanation Andrew presented relied on the fact that our scenario has always had Jill in her spacecraft travelling at a constant speed. In other words Special Relativity applied – Special because it is for the special case where there is no acceleration. Yet to return to her starting point, Jill must have decelerated at her destination and then accelerated again. Applying principles of General Relativity (where acceleration is accounted for) to such a case does resolve the paradox. Whichever point of view you take – Jack’s or Jill’s, Jill always arrives back on Earth younger than Jack.
Thank you Andrew for a well-presented talk and I wish I could understand more of it. Maybe, maybe, some time I will get my head round it.
For a fuller description of the various explanations for the paradox, look at the Wikipedia article
https://en.wikipedia.org/wiki/Twin_paradox
Talk given by FAS member Andrew Collins
Post written by Katherine Rusbridge
Aug 2017
